EDK

Project Euler

Project Euler (named after Leonhard Euler) is a website dedicated to a series of computational problems intended to be solved with computer programs.The project attracts adults and students interested in mathematics and computer programming. Since its creation in 2001 by Colin Hughes, Project Euler has gained notability and popularity worldwide. (Wikipedia)

Problem 1: Multiples of 3 or 5

"If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 1000."

This problem was a good way to get back into the swing of things after a few months of not touching Java. I approached this by implementing a counter for loop which ensured that our range never exceeded 1000. Moreover, whenever the remainder of our counter variable equalled 0 when divided by one of our natural numbers (3 or 5), our if statement would distinguish it as a multiple and add it to our sum variable.

Problem 2: Even Fibonacci Numbers

"Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms."

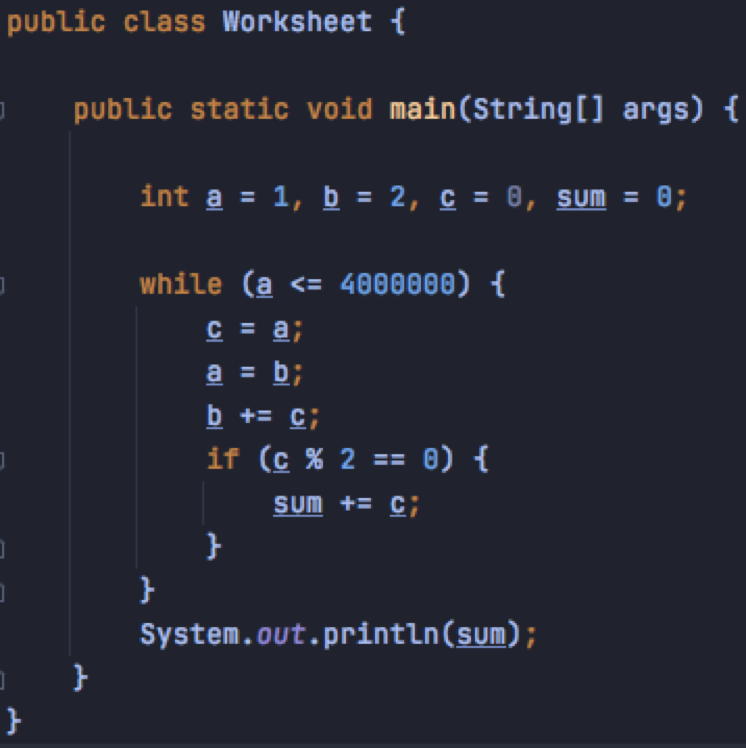
I began this problem by establishing the rules surrounding the Fibonacci sequence -- (Fn​ = Fn − 1​ + Fn − 2​ in this instance: F0 ​= 1 & F1 ​= 2). This allowed me to declare the first two variables (a representing F0 and b representing F1). From here I decided to use a while loop as I was unsure how many terms we would end up with, however, also respected our maximum range of 4,000,000 by ensuring we exited the loop once variable a reached it. Furthermore, so that our sum was a culmination of only even numbers, I implemented an if statement that tested for this.